有向图中的Tarjan算法个人理解-创新互联

Tarjan算法主要是解决强连通分量，双连通分量，割点和桥，求最近公共祖先（LCA）等问题的。

创新互联服务项目包括郁南网站建设、郁南网站制作、郁南网页制作以及郁南网络营销策划等。多年来，我们专注于互联网行业，利用自身积累的技术优势、行业经验、深度合作伙伴关系等，向广大中小型企业、政府机构等提供互联网行业的解决方案，郁南网站推广取得了明显的社会效益与经济效益。目前，我们服务的客户以成都为中心已经辐射到郁南省份的部分城市，未来相信会继续扩大服务区域并继续获得客户的支持与信任！前置知识：

连通分量：对于分量中任意两点u,v,必然可以从u到v，也可以从v到u。

强连通分量：就是极大连通分量。即一个连通分量加上任何一些点之后它都不是一个连通分量，那么就把它称为强连通分量。

例如此图，每一个被红色圈标注的部分都是一个强联通分量。

依此，我们能够把任意一个有向图经过缩点之后转化成一个有向无环图（DAG图）。

缩点：是指将所有强连通分量缩成一个点。

一：什么是Tarjan

简单来说，就是一个基于深度优先搜索的，用于求解图的连通性问题的算法。

二：Tarjan基础<一>：边：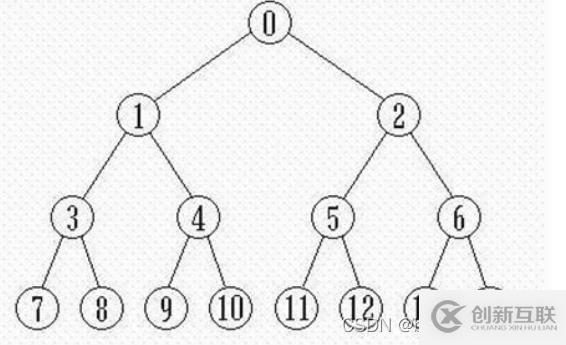

边有四类 ,以此图为例，对此树dfs：

1:树枝边：(x,y)例如(1,3)

2:前向边：(x,y)例如(1,7)

PS:树枝边是特殊的前向边。

3:后向边：(x,y)例如(7,1)

4:横叉边：(x,y)例如(9,8)

<二>：判断是都存在强连通分量：

1：存在后向边指向祖先节点。

2：走到了一个横叉边对应的节点，横叉边再走向祖先节点。

<三>：时间戳：

搜索时，按照搜索顺序给每个点一个编号（从小到大）。

对每个点定义两个时间戳：dfn[u]:表示遍历到U的时间戳。

low[u]：从u开始走，所能遍历到的最下位置，最靠近栈底。

因此可以发现：

对于时间戳dfn[]：

前向边:x

后向边:y

横向边:y

如果u是其所在强连通分量最高点，则dfn[u]==low[u].例如图中的⑦⑧等等。

三：Tarjan内容：求强连通分量过程:

void tarjan(int u)//每次传入一个点U，栈中存的不一定只是一个路径。
//栈中存的所有点都不是目前还没遍历完的强连通分量所有点
{
    dfn[u]=low[u]=++timestamp;//让dfn和low都等于时间戳
    stk[++top]=u;//把当前这个点加入栈
    in_stack[u]=1;//标记当前这个点在栈中
    
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];//取此边对应的点
        if(!dfn[j])//如果没有被遍历
        {
            tarjan(j);//遍历这个点
            low[u]=min(low[u],low[j]);//更新最小值
        }
        else if(in_stack[j])//在栈中，不是前向边
            low[u]=min(low[u],dfn[j]);
    }
    
    if(dfn[u]==low[u]) //u是强连通分量最高点
    {
        int y;
        ++scc_cnt;//强连通分量个数加一
        do 
        {
            y=stk[top--];
            in_stack=0;
            id[y]=scc_cnt;//标记这个点属于哪个强连通分量
        
        }while(y!=u);
        
    }
}

缩点：

1：遍历当前所有边

2：如果两个点不在同一个强连通分量，加一条新边。id[i]->id[j]

以此可以建立一个有向无环图。(DAG)

可以发现：连通分量编号递减顺序就是拓扑排序。

例题1：P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

对于此题分析：

1.奶牛的喜欢具有传递性，对于每一头奶牛对另一头奶牛的喜欢，我们用一条有向边相连，就是一个图上的问题。如果直接暴力--不好做。我们可以发现图中的强连通分量中所有奶牛互相喜欢，以此缩点，将每个强连通分量缩为一个点。

2.奶牛要想当明星，必须让除了自己以外的所有牛都喜欢他，因此这个强连通分量出度为0，如果有两个强连通分量出度为0，那么一定没有能当明星的奶牛，在这里不再做证明。

因此题目就转化为一个求出度为0的强连通分量的大小的问题。

代码如下：

#include#includeusing namespace std;
const int N=5e5+10;
int h[N],e[N],w[N],ne[N],dout[N],dfn[N],low[N],n,m,idx,time_table,scc_cnt,stacks[N],id[N],_size[N];
int top;
bool in_stacks[N];

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++time_table;
    stacks[++top]=u;
    in_stacks[u]=1;
    
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(!dfn[j])
        {
            tarjan(j);
            low[u]=min(low[u],low[j]);
        }
        else if(in_stacks[j])
        {
            low[u]=min(low[u],dfn[j]);
        }
    }
    
    if(dfn[u]==low[u])
    {
        int y;
        ++scc_cnt;
        do
        {
            y=stacks[top--];
            id[y]=scc_cnt;
            in_stacks[y]=0;
            _size[scc_cnt]++;
        }while(u!=y);
    }
    
}

int main()
{
    scanf("%d%d",&n,&m);
    
    memset(h,-1,sizeof(h));
    while(m--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
    }
    
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            tarjan(i);
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=h[i];~j;j=ne[j])
        {
            int k=e[j];
            int a=id[i],b=id[k];
            if(a!=b)
            {
                dout[a]++;
            }
        }
    }
    
    int zero=0,res=0;
    for(int i=1;i<=scc_cnt;i++)
    {
        if(!dout[i])
        {
            zero++;
            res=_size[i];
            if(zero>1)
            {
                res=0;
                break;
                
            }
        }
    }
    
    cout<

例题2：[USACO5.3]校园网Network of Schools对于此题，读题可知A->B为有向图，因此转化为图论问题。
不论我们给哪个学校发送新软件，它都会到达其余所有的学校
由此可知，比如A->B,B>C,就可以得出A->C。
分析问题：第一问求接受新软件副本的最少学校数目。
我们可以自行画图即可知道，这一问就是入度为0的点的个数，因为过于简单，不再多说。
第二问：计算最少需要增加几个扩展，使得不论我们给哪个学校发送新软件，它都会到达其余所有的学校。
对于此问，我们先有一个大致猜想为max(起点数，终点数).
证明：
将起点集合记为P，终点集合记为Q，对于此问可以发现起点与终点相当于对称，不论P>=Q还是P<=Q得出结果必定相同。因此，我们设P<=Q
一：如果|P|=1则这个起点可以走到任何终点，我们只需将每个终点反向连边即可，则结果为|Q|。
二：如果|P|>1,则|Q|>|P|>1
我们必然可以找到P1->Q1,P2->Q2.
我们对Q1->P1连接一条边，为了保证Q1和P1的性质，将其从图中去掉，则|P'|=|P|-1,|Q'|=|Q|-1
一共需要去掉|P|-1次，集合大小每次也在减一，需要加上的边数=|Q|-(|P|-1)+(|P|-1)=|Q|
得证。
AC代码：
#include#includeusing namespace std;
const int N=1e5+10;
int h[N],ne[N],e[N],id[N],idx,n,dfn[N],low[N],cnt,top,din[N],dout[N];
int stk[N],time_table;
bool st[N];

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++time_table;
    stk[++top]=u;
    st[u]=1;
    
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(!dfn[j])
        {
            tarjan(j);
            low[u]=min(low[u],low[j]);
        }
        else if(st[j]) low[u]=min(low[u],dfn[j]);
    }
    
    if(dfn[u]==low[u])
    {
        ++cnt;
        int y;
        do 
        {
            y=stk[top--];
            st[y]=0;
            id[y]=cnt;
        }while(y!=u);
    }
}

int  main()
{
    cin>>n;
    
    memset(h,-1,sizeof(h));
    for(int i=1;i<=n;i++)
    {
        int t;
        while(cin>>t,t)
        {
            add(i,t);
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i])
        {
            tarjan(i);
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=h[i];~j;j=ne[j])
        {
            int k=e[j];
            int a=id[i],b=id[k];
            if(a!=b)
            {
                dout[a]++,din[b]++;
            }
        }
    }
    
    int sum1=0,sum2=0;
    for(int i=1;i<=cnt;i++)
    {
        if(!din[i]) sum1++;
        if(!dout[i]) sum2++;
    }
    
    cout<
例题3：P3387 【模板】缩点此题重在掌握重新建图以及哈希表的判重方式。
#include#include#includeusing namespace std;
const int N=2e5+10;
int h[N],e[N],ne[N],d[N],idx,v[N],hs[N];
int time_table,dfn[N],low[N];
int stk[N],top,scc_cnt,id[N],siz[N];
bool in_stk[N];
int din[N];

void add(int h[],int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void tarjan(int u)
{
    dfn[u]=low[u]=++time_table;
    stk[++top]=u;
    in_stk[u]=1;
    
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(!dfn[j])
        {
            tarjan(j);
            low[u]=min(low[j],low[u]);
        }
        else if(in_stk[j]) 
        {
            low[u]=min(low[u],dfn[j]);
        }
    }
    
    if(dfn[u]==low[u])
    {
        int y;
        ++scc_cnt;
        do
        {
            y=stk[top--];
            in_stk[y]=0;
            id[y]=scc_cnt;
            siz[scc_cnt]+=v[y];
        }while(u!=y);
    }
}

int q[N];

void DAG()
{
    int hh=0,tt=-1;

    for(int i=1;i<=scc_cnt;i++)
    {
        if(!din[i])
        {
            q[++tt]=i;
            d[i]=siz[i];
        }
    }
    
    while(hh<=tt)
    {
        int t=q[hh++];
        
        for(int i=hs[t];~i;i=ne[i])
        {
            int j=e[i];
            d[j]=max(d[j],d[t]+siz[j]);
            din[j]--;
            if(!din[j])
                q[++tt]=j;
        }
    }
}

int st[N];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    
    for(int i=1;i<=n;i++) cin>>v[i];
    
    memset(h,-1,sizeof(h));
    memset(hs,-1,sizeof(hs));
    while(m--)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(h,a,b);
    }
    
    for(int i=1;i<=n;i++)
        if(!dfn[i]) 
            tarjan(i);
    
    unordered_sets;
    for(int i=1;i<=n;i++)
    {
        for(int j=h[i];~j;j=ne[j])
        {
            int k=e[j];
            int a=id[i],b=id[k];
            long long hash=a*100000ll+b;
            if(a!=b && !s.count(hash))
            {
                add(hs,a,b);
                din[id[k]]++;
                s.insert(hash);
            }
        }
    }
    
    DAG();
    
    int maxx=-1;
    for(int i=1;i<=n;i++)
        maxx=max(maxx,d[i]);
    cout<
例题4：P2272 [ZJOI2007]大半连通子图首先读懂题意：
1：何谓半连通？
一个有向图 G=(V,E) 称为半连通的 (Semi-Connected)，如果满足：∀u,v∈V，满足 u→v 或 v→u，即对于图中任意两点 u,v，存在一条 u 到 v 的有向路径或者从 v 到 u 的有向路径。
题目中这样描述，形象地说就是只要一个点可以走到另一个点就是半连通的。特别的，强连通分量也属于半连通 。
2：何谓半连通图？
一个图中所有点半连通。
3：何谓半连通子图？
半连通图的子集。
4：何谓大半连通子图？
在半连通子图中具有最多点数的图。
通过上述分析，想必题目大意已经明白了。
接下来思考解决方式。
一：暴力
凡是题目皆可暴力。
我们可以从每一个点开始找连通子图，从而找到大连通子图，但显然，这种方式是不可取的。
二：优化
优化1：我们可以发现强连通分量属于半连通的，对于一个强连通分量，在此题目中各个点含义没什么区别，因此对其可以缩点。
优化2：对于已经缩点之后的图，我们必然得到一个DAG图，因此，要想找到大的半连通子图，起点必从入度为0的点开始，因此我们不必从每个起点开始，只需找din[]==0的点开始即可。
优化3：对于构建DAG图时我们会遇到两个点之间有很多边的问题，可以应用例三中的hash判重。
优化4：对于求大点，我们不必一直加，用树形dp思想即可。
由此我们可以解决此问题，剩下的就是代码功底啦！
你是否还在寻找稳定的海外服务器提供商？创新互联www.cdcxhl.cn海外机房具备T级流量清洗系统配攻击溯源，准确流量调度确保服务器高可用性，企业级服务器适合批量采购，新人活动首月15元起，快前往官网查看详情吧
            

            网站名称：有向图中的Tarjan算法个人理解-创新互联            

            当前路径：http://ahjierui.cn/article/dcshso.html


    
        其他资讯
        
            
                    linux命令置换 linux切换命令行界面快捷键
                

                    java编写app代码 java 写app
                

                    手机卡怎么添加主站域名 手机号主卡怎么设置
                

                    C语言函数思维导图打印 c语言的思维
                

                    服务器装什么系统比较安全 服务器装什么系统比较安全好用

有向图中的Tarjan算法个人理解-创新互联

其他资讯

公司服务热线